ADFGVX加密算法

2.6k-
小作业
C++QT作业加密算法
本文最后更新于2 年前，文中所描述的信息可能已发生改变。

课堂小作业，实现古老的ADFGVX加密算法

这次的作业要求是完成 ADFGVX 加密算法，做一个可以加密、解密的小应用。要了解 ADFGVX 加密算法，首先得介绍一下 Polybius 加密算法。（其实以下介绍纯纯照搬老师给的pdf）

ADFGVX密码简介^1 ​

Polybius 密码 ​

Polybius 密码也称棋盘密码，是利用波利比奥斯方阵（Polybius Square）进行加密的密码方式。

假设我们需要发送明文消息“Attack at once”，用一套秘密混杂的字母表填满波利比奥斯方阵，像是这样：

ADFGX
Abtalp
Ddhozk
Fqfvsn
Ggjcux
Xmrewy

i 和 j 视为同一个字母，使字母数量符合 5 × 5 格。之所以选择这五个字母，是因为它们译成摩斯密码时不容易混淆，可以降低传输错误的机率。使用这个方格，找出明文字母在这个方格的位置，再以那个字母所在的行名称和列名称代替这个字母。

可将该消息转换成处理过的分解形式。

明文：A T T A C K A T O N C E

密文：AF AD AD AF GF DX AF AD DF FX GF XF

A、D、F、G、X 也可以用数字 1、2、3、4、5 来代替，这样密文就成了：

13 12 12 13 43 25 13 12 23 35 43 53

ADFGX 密码 ​

1918年，第一次世界大战将要结束时，法军截获了一份德军电报，电文中的所有单词都由 A、D、F、G、X 五个字母拼成，因此被称为 ADFGX 密码。

ADFGX 密码是 1918 年 3 月由德军上校 FritzNebel 发明的，是结合了 Polybius 密码和置换密码的双重加密方案。A、D、F、G、X 即 Polybius 方阵中的前5个字母。

明文：A T T A C K A T O N C E

经过Polybius变换：AF AD AD AF GF DX AF AD DF FX GF XF

下一步，利用一个移位密钥加密。假设密钥是 “CARGO”，将之写在新格子的第一行。再将上一阶段的密文按行写进新方格里。

CARGO
AFADA
DAFGF
DXAFA
DDFFX
GFXFX

最后，密钥按照字母表顺序 “ACGOR” 排序，再按照此顺序依次读出每个字母下面的整列，形成新密文。如下：

FAXDF ADDDG DGFFF AFAXX AFAFX

在实际应用中，移位密钥通常有两打字符那么长，且分解密钥和移位密钥都是每天更换的。

ADFGVX 密码 ​

在 1918 年 6 月，再加入一个字 V 扩充。变成以 6 × 6 格共 36 个字符加密。这使得所有英文字母（不再将 I 和 J 视为同一个字）以及数字 0 到 9 都可混合使用，这次增改是因为以原来的加密法发送含有大量数字的消息有问题。

程序使用 ​

了解完算法，先直接来看看我所实现的小应用，Yuumi’s ADFGVX Cypher。

该程序为ADFGVX密码的实现，已上传Github。重要文件结构如下：

CODE
│  README.md		// 此文件
│
├─myCypher
│      adgfvxalgo.cpp		// 密码类
│      adgfvxalgo.h		// 密码头文件
│      CMakeLists.txt		// CMakeList
│      main.cpp			// 主程序
│      widget.cpp		// 界面程序
│      widget.h			// 界面头文件
│
└─release
       ChangeAlphabet.txt	// 预留的密码表更改文件
       myCypher.exe		// 可执行程序

release 目录下的 myCypher.exe 为程序的可执行文件，下文将介绍其使用方法。

运行环境 ​

  • Windows 64位操作系统

使用方法 ​

  1. 运行程序：双击打开 myCypher.exe ，看到界面，则运行成功。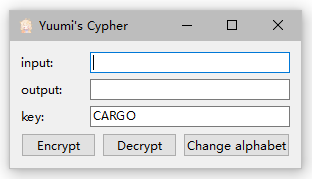

    image-20221104161910699

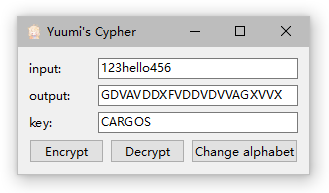
  2. 明文加密：在 input 框中输入需要加密的明文信息，在 key 框中输入置换密码的密钥。点击 Encrypt ，在 output 框中会出现加密结果。

    • 明文仅可输入英文字母或数字，大写字母将自动转换为小写字母；
    • 密钥仅可输入英文字母，小写字母将自动转换为大写字母；
    • 若未输入密钥，则将使用默认密钥 CARGO 进行加密。
    image-20221104162849897

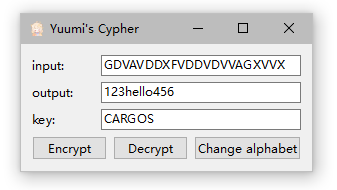
  3. 密文解密：在 input 框中输入需要解密的密文信息，在 key 框中输入置换密码的密钥。点击 Decrypt ，在 output 框中会出现解密结果。

    • 仅可输入符合ADFGVX密码要求的密文（只包含“ADFGVX”六个大写字母）；
    • 密钥要求同上。
    image-20221104163444089

  4. 更改ADFGVX密码表：点击 Change alphabet ，弹出框中选择密码表文件，即可切换密码表。

    • 密码表需为 .txt 文件，内容为26个英文字母与数字0~9的随意排列。例如：

      wxydefghi123klmn567optuvcba0489jqrsz

    • 若密码表未更改，则默认为：

      xyzdefghiklmnopqrstuvwcba0123456789j

开发设计 ​

该程序使用QT框架，C++编写。

开发环境 ​

  • QT 6.4.0
  • MinGW 11.2.0
  • C++ 11

算法和程序设计 ​

ADFGVX加密算法是一种结合了扩展的Polybius密码和置换密码的双重加密方案，具体算法内容参考开头的介绍。

程序设计 ​

由于ADFGVX加密算法中的密码表、置换密钥均为人为设置、可以改动的变量，且密码表不常更换、置换密钥较常更换。因此除了输入、输出框外，另外设计了密钥输入框和更改密码表按钮。加密算法类成员函数设计如下(adgfvxalgo.h)：

cpp
ADGFVXalgo(string cargo);   //构造函数
void encrypt();     // 加密操作
void decrypt();     // 解密操作
void setMessage(string str);    // 设置明文
void setCypher(string str);     // 设置密文
void setCargo(string str);      // 设置密钥
void setADGFVXinput(string str);    // 设置密码表
string getCypher();     // 获取密文
string getMessage();    // 获取明文

加密设计 ​

为了快速查找到明文在密码表中对应的密文，我先将字符串类型的密码表转换为map：

cpp
// 建表
multimap<char, pair<char, char>> table;
char charList[6] = {'A', 'D', 'F', 'G', 'V', 'X'};
int i=0, j=0, pos=0;
for(i = 0; i < 6; i++) {
    for(j = 0; j < 6; j++) {
        table.insert({ADGFVXtable[pos], {charList[i], charList[j]}});
        pos++;
    }
}

接着通过查找转换好的密码表来输出第一道密文到 midCypher 中，便完成了扩展的Polybius密码算法：

cpp
// polybius密码
vector<char> midCypher;
for (auto alpha: input){
    auto iter = table.find(alpha);
    midCypher.push_back(iter->second.first);
    midCypher.push_back(iter->second.second);
}

最后用sort函数得到密钥的字典序，以 pos 来标明字典序位置，输出列到 cypher 即可。

cpp
// 置换密码
string str = CARGOinput;
sort(str.begin(), str.end());
pos = 0;
for (auto ch: str){
    pos = CARGOinput.find(ch);
    for (i=0; i < midCypher.size()/CARGOinput.length(); i++)
        cypher.push_back(midCypher[i * CARGOinput.length() + pos]);
}

但是！如果polybius得到的第一道密文长度不能被密钥长度整除，当整除时会漏掉密文的最后几位。因此还需要考虑不整除的情况。因为在不整除的情况下，即“置换表格不能被填满”时，空缺的一定是最后一行右侧的位置。因此用 remainder 来保存余数，若为密钥的前 remainder 列，则输出 密文长度/密钥长度+1 个字母；若不为前 remainder 列，则输出 密文长度/密钥长度 个字母即可。

cpp
// 置换表格不满
int remainder = midCypher.size()%CARGOinput.length();
string str = CARGOinput;
sort(str.begin(), str.end());
pos = 0;
for (auto ch: str){
    pos = CARGOinput.find(ch);
    if (pos < remainder)
        for (i=0; i < midCypher.size()/CARGOinput.length()+1; i++)
            cypher.push_back(midCypher[i * CARGOinput.length() + pos]);
    else
        for (i=0; i < midCypher.size()/CARGOinput.length(); i++)
            cypher.push_back(midCypher[i * CARGOinput.length() + pos]);

解密设计 ​

加密的过程是 polybius -> 置换，因此解密过程为 反置换 -> 反polybius。建表操作、反polybius和加密基本相同，不过要将map中的键值反转一下。置换解密的可整除部分也大差不差，就是输出也需要翻转一下，是从字典序到密钥原来的顺序。

但是不可整除的置换解密就要复杂一点。如果不可整除，例如明文为 12hello ，密钥为 CRAGOS ，则第一道密文为 VF VG DD AV DV DV FD ，放入置换列表后会看到：

CRAGOS
VFVGDD
AVDVDV
FD

置换后输出为 VD VAF GV DD FVD DV 。可以发现无法直接用数学循环找到某个字母下的列，因为每一列的长度是不一样的。我的解决方案为：因为我们知道密文的长度、知道具体的密钥，所以我们必然知道会多出来几个字母（余数有几位），以及置换前后的密钥列顺序。因此我们只需要把 "除了前(余数)位的列" 以外的所有列 的最后都填上某个字符，就可以保证置换列表是一个满列表，从而循环输出了。因为知道余数是多少，且密文只会有ADFGVX，因此不会对正确性造成影响。

为此我新建了一个vector来保存哪些列为密钥的前(余数)列，在非前(余数)列的末尾加上’0’，并在顺序输出时无视’0’，即可成功反置换回来。

cpp
vector<int> temp;
for (i=0; i<remainder; i++) {
    pos = str.find(CARGOinput[i]);
    temp.push_back(pos);
}
for (i=0; i<CARGOinput.length(); i++){
    if (find(temp.begin(), temp.end(), i) != temp.end())
        continue;
    input.insert(input.begin() + (i * (cypher.size()/CARGOinput.length()+1)) + cypher.size()/CARGOinput.length(), '0');
}
for (i=0; i<input.size()/CARGOinput.length(); i++){
    for (auto ch: CARGOinput){
        pos = str.find(ch);
        char tempChar = input[pos * (input.size()/CARGOinput.length()) + i];
        if (tempChar == '0') continue;
        else    midCypher.push_back(tempChar);
    }
}

后记 ​

以上是我笨笨的解决办法，写加密、解密的时候是晚上，整得自己头昏脑涨的。我知道大家肯定有更简单、更合适的解决办法，期待你的留言哦！

第一次在 github 上发布 release，虽然只是个小小应用，但也算是踏出了第一步吧。继续加油！

smallCCompiler
摄影与生活
© 2021 - 2024
Yuumi
由 Valaxy v0.18.5 驱动 | 主题 - Yun v0.18.5